La régression linéaire

Aujourd’hui nous allons parler de régression linéaire, l’une des plus anciennes méthodes d’apprentissage statistique. Nous commençons donc volontairement par une piste verte pour s’échauffer et partir sur une base simple dont vous avez probablement tous déjà entendu parler dans votre cursus.

Dans cet article, nous aborderons dans un premier temps l’aspect théorique de la régression linéaire, avant de donner quelques exemples d’implémentation avec les outils les plus couramment utilisés.

Théorie

L’idée de la régression linéaire est simple : il s’agit de faire l’approximation qu’entre un ensemble de données et un autre il existe une relation “linéaire”, c’est-à-dire du type $y=ax+b$, qui peut être représentée par une droite (cf. figure ci-dessous).

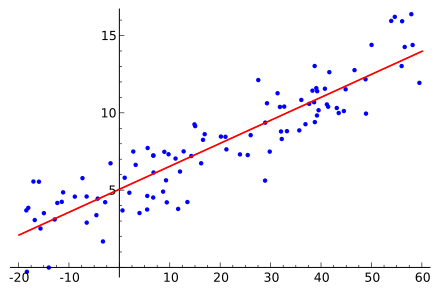
Source : https://commons.wikimedia.org/wiki/File:Linear_regression.svg?uselang=frv

Pour ne pas rebuter les moins matheux d’entre vous, prenons d’emblée un exemple que l’on utilise quasi-quotidiennement en anesthésie-réanimation : le poids idéal théorique. Cette formule a été développé initialement en 1983 par J. Daniel Robinson et ses collègues pour adapter la posologie des molécules prescrites¹. Elle se base sur une régression linéaire des tables de poids idéaux publiés par la compagnie d’assurance Metropolitan Life².

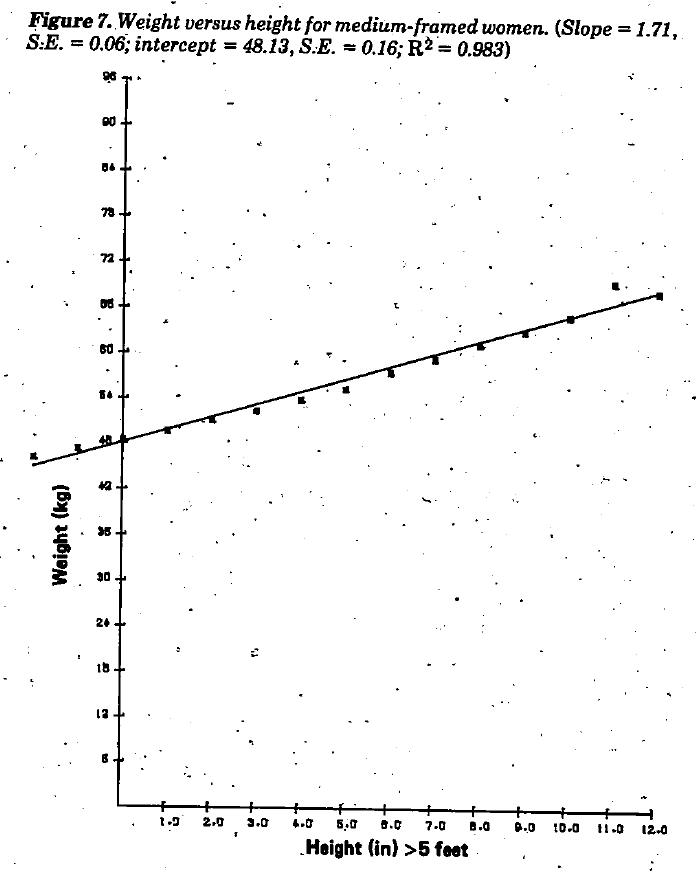
Régression linéaire donnant le poids idéal des femmes de stature intermédiaire¹.

Les tables originales n’étant plus disponibles, nous utiliserons leur version actualisée de 1999 :

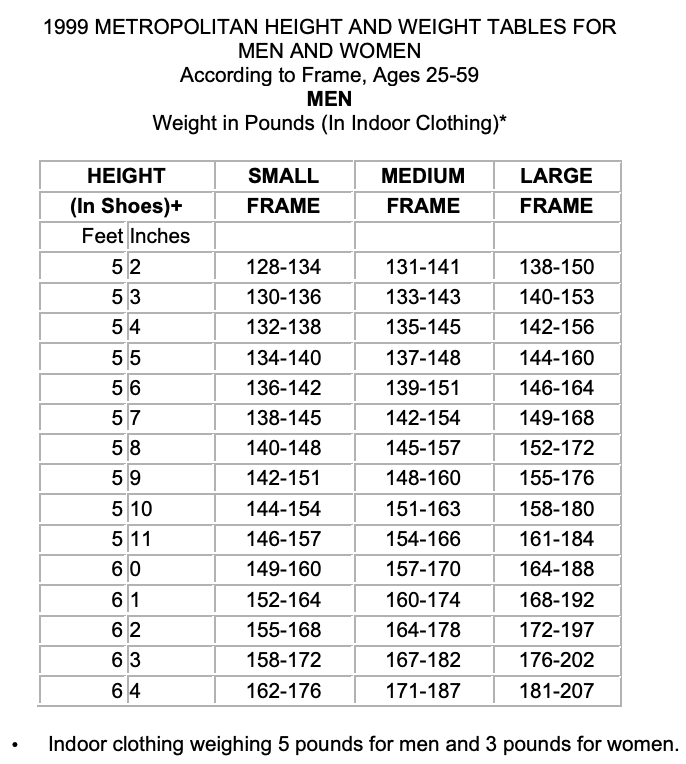
Après avoir converti les tailles en cm, les poids en kg, et en ne considérant que la taille médiane des femmes de stature intermédiaire, nous obtenons le tableau de valeurs suivant :

Ce qui graphiquement donne le résultat suivant :

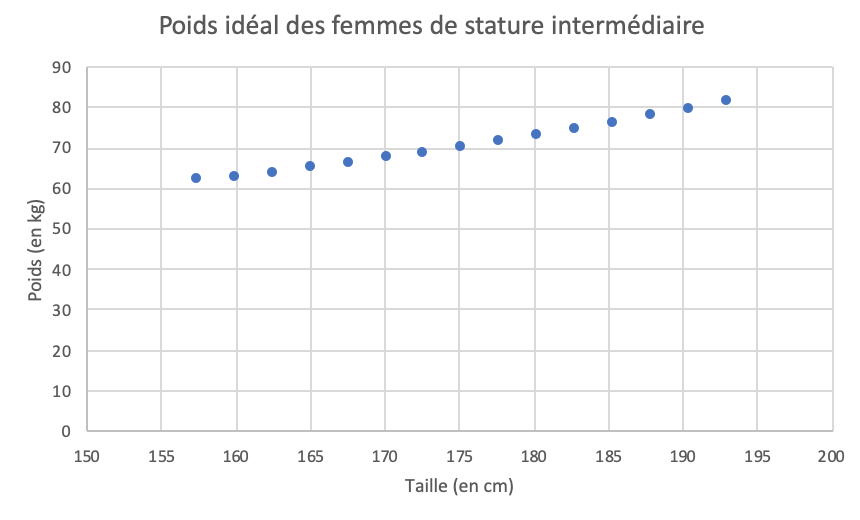
On voit que la taille minimale est 157 cm, donc par exemple pour une femme de 150 cm on ne peut pas se référer à la table pour avoir une estimation du poids idéal. C’est là que la régression linéaire entre jeu : nous allons trouver la droite qui permet d’estimer au mieux ces points du graphique.

Pour cela, il s’agit de trouver les paramètres $a$ et $b$ qui minimisent l’erreur que l’on fait lorsqu’on fait l’approximation que le lien entre le poids $y$ et la taille $x$ s’écrit de la forme $y=ax+b$. Dans notre exemple, si l’on choisit $a = 0.5$ et $b = -18$, on obtient les valeurs suivantes :

Ce qui donne graphiquement la courbe rouge ci-dessous :

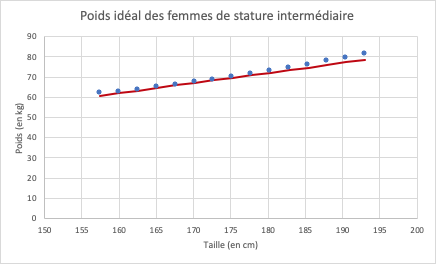
Ceci semble être une approximation convenable, mais on ne sait pas si c’est la “meilleure”, c’est-à-dire minimisant l’erreur de mesure. Plusieurs méthodes existent, mais la plus connue et la plus utilisée dans ce contexte reste la méthode des moindres carrés. Sans rentrer dans les détails mathématiques ici, cette méthode permet de calculer exactement la solution qui minimise l’erreur quadratique. Toujours dans le contexte de notre exemple, si l’on fait la différence entre les points bleus et la courbe rouge, nous obtenons les valeurs de l’avant-dernière colonne du tableau suivant :

Les valeurs de la dernière colonne ne sont autre que celles de l’avant-dernière colonne mises au carré (d’où le nom de quadratique). La somme de cette dernière colonne est ce qu’on appelle l’erreur quadratique et s’élève ici à 16,51. En utilisant la méthode des moindres carrés, on trouve que les valeurs optimales sont environ $a = 0.54$ et $b = -25.6$. Ceci donne les valeurs suivantes :

On constate que la valeur de l’erreur quadratique est plus faible qu’avec nos valeurs initiales, ici 4,60. On peut également constater que la droite épouse mieux les valeurs graphiquement :

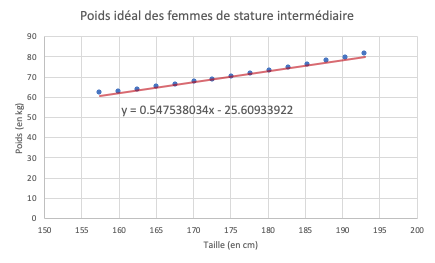
Implémentation

Tableurs

• Excel
• Google sheets
• Open Office

Langages de programmation

• R
• Python

Sources

1. Robinson JD, Lupkiewicz SM, Palenik L, Lopez LM, Ariet M. Determination of ideal body weight for drug dosage calculations. Am J Hosp Pharm. 1983 Jun;40(6):1016-9. PMID: 6869387.
2. Metropolitan Life Insurance Company. Desirable weight in indoor clothing. Statistical bulletin no. 40.1959 Nov-Dec.